%%file requirements.txt
numpy
matplotlib
numba
astropy!pip install -q pip --upgrade
!pip install -q -r requirements.txt# make sure pylab runs inline when using the notebook
%matplotlib inline
import numpy as np
import pylab as plt
light_minimal = {
'font.family': 'serif',
'font.size': 14,
"axes.titlesize": "x-large",
"axes.labelsize": "large",
'axes.edgecolor': '#666666',
"xtick.direction": "out",
"ytick.direction": "out",
"xtick.major.size": "8",
"xtick.minor.size": "4",
"ytick.major.size": "8",
"ytick.minor.size": "4",
'xtick.labelsize': 'small',
'ytick.labelsize': 'small',
'ytick.color': '#666666',
'xtick.color': '#666666',
'xtick.top': False,
'ytick.right': False,
'axes.spines.top': False,
'axes.spines.right': False,
'image.aspect': 'auto'
}
plt.style.use(light_minimal)Code typing in Python¶
Python >= 3.5
Python is a dynamically typed language¶
Variables have implicit types
types can change with a simple assignment
a = 5 # integer
a = "text" # stringPython >= 3.5 concept of type annotations
add hints about the expected type of a parameter
a: int = 5
b: str = "text"Typing Examples¶
def scale(scalar, vector):
return [scalar * num for num in vector]
new_vector = scale(2.0, [1.0, -4.2, 5.4])Vector = list[float]
def scale(scalar: float, vector: Vector) -> Vector:
return [scalar * num for num in vector]
new_vector = scale(2.0, [1.0, -4.2, 5.4])ℹ️ Note how readable the second version becomes.
Function Annotations¶
The following adds annotations to your function
Vector = list[float]
def scale(scalar: float, vector: Vector) -> Vector:
return [scalar * num for num in vector]
scale.__annotations__{'scalar': float, 'vector': list[float], 'return': list[float]}One can use these to enforce variable types. (not the default)
Documentation is not “redundant” (bad practice example)
def func(a: IpAddress, b: List[Users], c: str) -> float: ...
Variable Annotations¶
a: int = 5
b: str = "text"
__annotations__{'a': int, 'b': str}One can use these to enforce variable types. (not the default)
a = "text" # what happens?
a: "dummy quantity" = 5 # Does it work? What could this mean?⚠️ not making a statically typed language out of Python
How to manually check types¶
# pseudo code
func: Callable(args: Sequence[Any], kwargs: Dict[str, Any]) = ...
sig = inspect.signature(func: Callable)
for value, (name, pardef) in zip(args, sig.parameters.items()):
try:
valid = isinstance(value, pardef.annotation)
except GenericAnnotationTypeError: # e.g. List[...], Sequence[...]
valid = isInstanceGenericType(value, pardef.annotation) # complex function to write
except NoAnnotationError: # ⚠️ "NoAnnotationError" does not exists
valid = True
else:
valid = False
if not valid:
raise RuntimeError(f"TypeCheck {name:s}: got {value} not of type {pardef.annotation}.")
result = func(*args, **kwargs)
if not isInstanceGenericType(result, sig.return_annotation):
raise RuntimeError(f"TypeCheck returned value: got {value} not of type {sig.return_annotation}.")from typing import Any, Sequence, Callable
from itertools import cycle
import inspect
Vector = list[float]
def scale(scalar: float, vector: Vector) -> Vector:
return [scalar * num for num in vector]
def AssertInstanceGenericType(name: str, value: Any, annotation: type) -> None:
if annotation == inspect._empty: # empty annotation
return
try:
if not isinstance(value, annotation):
raise RuntimeError(f"TypeCheck {name:s}: got {value} not of type {annotation}.")
except TypeError: # e.g. List[...], Sequence[...]
orig, what = annotation.__origin__, annotation.__args__
if not isinstance(value, orig):
raise RuntimeError(f"TypeCheck {name:s}: got {value} not of type {annotation}.")
for e, (subval, subw) in enumerate(zip(value, cycle(what))):
AssertInstanceGenericType(f"{name:s}[{e:d}]", subval, subw)
def isinstanceGenericType(name: str, value: Any, annotation: type, verbose: bool = True) -> bool:
try:
AssertInstanceGenericType(name, value, annotation)
return True
except RuntimeError as err:
if verbose:
print(err)
return False
def assert_types(func: Callable,
*args: Sequence[Any],
**kwargs: dict[str, Any]) -> Any:
sig = inspect.signature(func)
for value, (name, pardef) in zip(args, sig.parameters.items()):
AssertInstanceGenericType(name, value, pardef.annotation)
result = func(*args, **kwargs)
AssertInstanceGenericType("returned value", result, sig.return_annotation)
return resultisinstanceGenericType('dummy', 2.0, int)TypeCheck dummy: got 2.0 not of type <class 'int'>.
FalseisinstanceGenericType('dummy', 2, int)TrueisinstanceGenericType('dummy', [2, 3.0], list[int])TypeCheck dummy[1]: got 3.0 not of type <class 'int'>.
FalseisinstanceGenericType('dummy', [2, 3.0], list[int | float])---------------------------------------------------------------------------
TypeError Traceback (most recent call last)
Input In [13], in <cell line: 1>()
----> 1 isinstanceGenericType('dummy', [2, 3.0], list[int | float])
TypeError: unsupported operand type(s) for |: 'type' and 'type'assert_types(scale, 2.0, [1.0, -4.2, 5.4])[2.0, -8.4, 10.8]assert_types(scale, 2.0, [1.0, -4.2, 5])---------------------------------------------------------------------------
TypeError Traceback (most recent call last)
Input In [9], in AssertInstanceGenericType(name, value, annotation)
14 try:
---> 15 if not isinstance(value, annotation):
16 raise RuntimeError(f"TypeCheck {name:s}: got {value} not of type {annotation}.")
TypeError: isinstance() argument 2 cannot be a parameterized generic
During handling of the above exception, another exception occurred:
RuntimeError Traceback (most recent call last)
Input In [15], in <cell line: 1>()
----> 1 assert_types(scale, 2.0, [1.0, -4.2, 5])
Input In [9], in assert_types(func, *args, **kwargs)
37 sig = inspect.signature(func)
38 for value, (name, pardef) in zip(args, sig.parameters.items()):
---> 39 AssertInstanceGenericType(name, value, pardef.annotation)
41 result = func(*args, **kwargs)
42 AssertInstanceGenericType("returned value", result, sig.return_annotation)
Input In [9], in AssertInstanceGenericType(name, value, annotation)
20 raise RuntimeError(f"TypeCheck {name:s}: got {value} not of type {annotation}.")
21 for e, (subval, subw) in enumerate(zip(value, cycle(what))):
---> 22 AssertInstanceGenericType(f"{name:s}[{e:d}]", subval, subw)
Input In [9], in AssertInstanceGenericType(name, value, annotation)
14 try:
15 if not isinstance(value, annotation):
---> 16 raise RuntimeError(f"TypeCheck {name:s}: got {value} not of type {annotation}.")
17 except TypeError: # e.g. List[...], Sequence[...]
18 orig, what = annotation.__origin__, annotation.__args__
RuntimeError: TypeCheck vector[2]: got 5 not of type <class 'float'>.How to enforce types ?¶
manually: (⚠️ Not recommended)
Rapidly complex to check all types and subtypes.
Not optimized checks will lead to significant overhead.
Maybe not worth apart from debugging phases.
With CI/CD: Type check and find common bugs (:thumbsup:)¶
Typing Pros & Cons...¶
Why? Increasing code
quality (for you to think about types)
readability (standard documentation; allowing automated checks)
improve IDEs and linters (as providing standard documentation)
cons
rapidly cumbersome, not always with useful predictable types
no standard to enforce types.
introduce a slight penalty in startup time.
Loosing Python’s flexibility
 A concept
A concept
an “object”
aka triangle
attributes (properties)
3 edges
edgecolor
facecolor ...
methods (functions)
get_edges
set_color
move_to ...
Important Vocabulary: object vs. class¶
a class is a definition, aka blueprint or template from which objects are created
an object is an entity instanciated from a class.
example:
import pylab as plt
r = plt.plot(range(10))
r
r contains objects of class Line2D (or matplotlib.lines.Line2D)
In python, everything is an object¶
sis an object from classstr
s = "some text"
s1 = s.strip() # remove leading/trailing spaces
su = s1.upper() # make uppercase
print(su)SOME TEXT
object<dot>method()
modules are objects too! (class module)
import numpy d = numpy.random.normal(0, 1, 100)as well as functions, code, even the running environment.
OOP example with Matplotlib¶
import pylab as plt
r = []
r.append( plt.plot(range(10)) )
r.append( plt.xlabel('measured') )
r.append( plt.ylabel('calculated') )
r.append( plt.title('Measured vs. Calculated') )
r.append( plt.grid(True) )
r
plt.plot(range(10))
plt.xlabel('measured')
plt.ylabel('calculated')
plt.title('Measured vs. Calculated')
plt.grid(True)
ax = plt.gca() # gca == get current axis
line = ax.lines[0]
line.set_marker('o')
plt.setp(line, color='g'); # set properties
How do we define our own classes / objects?¶
Let’s make a class “Vector”¶
Class Vector:
attrs: x, y, z
Methods: addition, scalar product, projection
class Vector(object):
def __init__(self):
passWhen a class defines an __init__() method, class instantiation automatically invokes __init__() for the newly-created class instance. So in this example, a new, initialized instance can be obtained by:
Note: Often, the first argument of a method is called self.
This is nothing more than a convention: the name self has absolutely no special meaning to Python.
Note, however, that by not following the convention your code may be less readable to other Python programmers, and it is also conceivable that a class browser program might be written that relies upon such a convention.
class Vector:
def __init__(self, x, y, z):
""" Constructor """
self.x, self.y, self.z = x, y, z
def sum(self, other):
""" add 2 vectors """
return Vector(self.x + other.x,
self.y + other.y,
self.z + other.z)
def scalar_prod(self, other):
""" product of 2 vectors """
return (self.x * other.x +
self.y * other.y +
self.z * other.z)a = Vector(1,0,0)
b = Vector(0,1,0)
print("a . b = ", a.scalar_prod(b))
print(a.sum(b)) #???a . b = 0
<__main__.Vector object at 0x11ba13eb0>
What’s wrong with print?
Print is equivalent to
str(a)ora.__str__()we need to define
__str__()
class Vector:
def __init__(self, x, y, z):
""" Constructor """
self.x, self.y, self.z = x, y, z
def sum(self, other):
""" add 2 vectors """
return Vector(self.x + other.x,
self.y + other.y,
self.z + other.z)
def scalar_prod(self, other):
""" product of 2 vectors """
return (self.x * other.x +
self.y * other.y +
self.z * other.z)
def __str__(self):
""" str representation """
return "Vector({s.x},{s.y},{s.z})".format(s=self)a = Vector(1,0,0)
b = Vector(0,1,0)
print("a . b = ", a.scalar_prod(b))
print(a.sum(b)) #???a . b = 0
Vector(1,1,0)
object.__repr__(self)
Called by the repr() built-in function and by string conversions (reverse quotes) to compute the “official” string representation of an object.
object.__str__(self)
Called by the str() built-in function and by the print statement to compute the “informal” string representation of an object.
What about checking that
x = Vector(1, 0, 0)
y = Vector(0, 1, 0)
z = Vector(0, 0, 1)
# x.scalar_prod(x).sum(y.scalar_prod(y))
x.scalar_prod(x) + y.scalar_prod(y) + 2 * x.scalar_prod(y) == x.sum(y).scalar_prod(x.sum(y))TrueOverloading operators¶
How would you implement ?
a.scalar_prod(a).sum(b.scalar_prod(b))wouldn’t be better to use
+and*operators ??
Special methods such as
__str____add__,__sub__,__mul__,__matmul__,__div__,__pow__, ... and many others see python datamodel
Exercise: Complete the Vector class¶
manage a string representation
handle common operators
+,–Implement a scalar product solution based on
*Implement vector product based on
@
# x ** 2 + y ** 2 + 2 * x * y == (x + y) ** 2class Vector(object):
def __init__(self, x, y, z):
self.x, self.y, self.z = x, y, z
def __repr__(self):
# String repr, called when >>> Vector([1,2,3]) <CR>
return self.__str__() + ", " + object.__repr__(self)
def __str__(self):
""" str representation """
return "Vector({s.x},{s.y},{s.z})".format(s=self)
def __add__(self, p):
if isinstance(p, Vector): # if p Vector, sum of p1*p2
return Vector(self.x + p.x, self.y + p.y, self.z + p.z)
return Vector(self.x + p, self.y + p, self.z + p)
def __mul__(self, p):
if isinstance(p, Vector): # scalar product p1*p2
return self.x * p.x + self.y * p.y + self.z * p.z
return Vector(self.x * p, self.y * p, self.z * p)
def __matmul__(self, p):
""" self @ p as vector product """
if not isinstance(p, Vector):
raise RuntimeError("second argument is not a Vector")
x = self.y * p.z - self.z * p.y
y = self.z * p.x - self.x * p.z
z = self.x * p.y - self.y * p.x
return Vector(x, y, z)
def __pow__(self, p):
return sum([self.x ** p, self.y ** p, self.z ** p])x = Vector(1, 0, 0)
y = Vector(0, 1, 0)
z = Vector(0, 0, 1)
xy = x * y
print("x.y = ", xy)
print(x)
x * x + y * y + x * y * 2 == (x + y) ** 2x.y = 0
Vector(1,0,0)
TrueBonus exercise¶
Generalize the class vector and all operations to N-dimensions (tip: you can use numpy arrays)
import numpy as np
class Vector(object):
def __init__(self, x):
self.x = np.atleast_1d(x)
def __repr__(self):
# String repr, called when >>> Vector([1,2,3]) <CR>
return self.__str__() + ", " + object.__repr__(self)
def __str__(self):
""" str representation """
return "Vector({s.x})".format(s=self)
def __add__(self, p):
if isinstance(p, Vector): # if p Vector, sum of p1*p2
return Vector(self.x + p.x)
return Vector(self.x + p)
def __mul__(self, p):
if isinstance(p, Vector): # scalar product p1*p2
return np.sum(self.x * p.x)
return Vector(self.x * p)
def __matmul__(self, p):
""" self @ p as vector product """
if not isinstance(p, Vector):
raise RuntimeError("second argument is not a Vector")
return Vector(x @ p.x)
def __pow__(self, p):
return sum(self.x ** p)x = Vector([1, 0, 0])
y = Vector([0, 1, 0])
z = Vector([0, 0, 1])
xy = x * y
print("x.y = ", xy)
print(x)
x * x + y * y + x * y * 2 == (x + y) ** 2x.y = 0
Vector([1 0 0])
TrueFunctions are objects too! they implement __call__¶
exercise: Create a “function”
interpof two sequencesx,ythatkeep in mind the input data
and when called with a sequence
xn, interpolates the datayn = y(xn)
ℹ️ There are two approaches possible (using a class or only functions)
💡 Don’t code the interpolation, use np.interp instead.
import numpy as np
import pylab as plt
class Interp:
def __init__(self, x, y):
self.x, self.y = x, y
def __call__(self, xn):
return np.interp(xn, self.x, self.y)
def interpfn(x, y):
def f(xn):
return np.interp(xn, x, y)
return fimport numpy as np
import pylab as plt
x = np.arange(10)
y = np.hstack([x[: 5] ** 2, 25 - 5 * x[5:]])
interp = Interp(x, y)
xn = np.linspace(0, 10, 20)
plt.plot(x, y, 'o-', lw=2)
plt.plot(xn, interp(xn), '.-')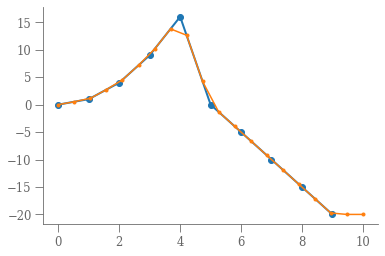
When to use classes or not?¶
Classes are useful tools.
Simple > complex > complicated.
Practicality beats purity.
Do not reinvent the wheel every time. When tools you already work: use & adapt them.
Readability counts!
Stop writing classes by Jack Diederich (30 min video)

Exercise: Coding the an IMF “package”¶
All mass functions share common properties
, how mass is frequently formed?
Probability distribution function
usually defined as broken power-laws
ℹ️ Some tips to come in the next slides
Class Inheritance: Establish relationships between objects.¶
Of course, a language feature would not be worthy of the name “class” without supporting inheritance. The syntax for a derived class definition looks like this:
class IMF(object):
mass = [0.1, 120.]
class Salpeter(IMF):
passf = Salpeter()
print(f.mass)[0.1, 120.0]
Execution of a derived class definition proceeds the same as for a base class. When the class object is constructed, the base class is remembered. This is used for resolving attribute references: if a requested attribute is not found in the class, the search proceeds to look in the base class. This rule is applied recursively if the base class itself is derived from some other class.
There’s nothing special about instantiation of derived classes: Salpeter() creates a new instance of the class. Method references are resolved as follows: the corresponding class attribute is searched, ascending up the chain of parent classes if necessary, and the method reference is valid if this yields a function object.
Derived classes may override methods of their base classes.
An overriding method in a derived class may in fact want to extend rather than simply replace the base class method of the same name. There is a simple way to call the base class method directly: just call IMF.methodname(self, *args, **kwargs). It is common to call the parent constructor in the derived class constructor:
def Salpeter(IMF):
def __init__(self, *args, **kwargs):
IMF.__init__(self, *args, **kwargs)or
def Salpeter(IMF):
def __init__(self, *args, **kwargs):
super().__init__(self, *args, **kwargs)Note that the above example is equivalent to doing nothing special and thus can be omitted (it is the implicit definition from inheritance)
The requirements are:
Computing the expected number of stars per mass bin
Computing the mass enclosed in a given mass range
Being able to draw random masses from an IMF
What is the average mass predicted by an IMF?
Below is a template of IMF class. Feel free to adapt.
class IMF(object):
"""
IMF object class
let you define an IMF as multiple power-laws.
attributes:
norm: norm of the function
"""
def __init__(self, *args, **kwargs):
"""
"""
pass
def get_enclosed_mass(self, Mmin, Mmax):
"""Get the enclosed mass over a given mass range.
"""
pass
def get_enclosed_Nstar(self, Mmin, Mmax):
"""Get the enclosed dN over a given mass range
"""
pass
def get_avg_mass(self, Mmin, Mmax):
""" get the avg mass over a given range """
pass
def getValue(self, m):
""" returns the value of the normalized IMF at a given mass m:
note: m can be an iterable
"""
pass
def random(self, N, massMin=None, massMax=None):
""" Draw samples from this distribution
Samples are distributed over the interval [massMin, massMax]
Interval is truncated to the IMF range definition if it extents beyond it.
(taken as is otherwise)
"""
pass
def __call__(self, m=None):
return self.getValue(m)Some common IMF¶
Below some definitions in terms of x the mass interval edges and a the power-law indices on each interval.
Kroupa2001
x = [0.01, 0.08, 0.5, 1., 150.] a = [0.7, -0.3, -1.3, -1.3]Kennicut
x = [0.1, 1., 120.] a = [-0.4, -1.5]Salpeter
x = [0.1, 120.] a = [-1.35]
Mathematical Background¶
An IMF is a probability density distribution function: where its integral is unity (by definition) gives use The function is continuous.
💡 The first task of the contructor will be to create a continous function from the broken power-law definition and to normalize it properly.
⚠️ when indexes of the different power-laws are in units of , -2.35 corresponds to a Salpeter IMF. But, sometimes you could find -1.35, which corresponds to an index defined in terms of .
From this, the fractional number of stars within an interval is the integral: and the mass is expectation of the distribution, The average mass over this interval is then
Drawing random samples
drawing random numbers from a given distribution can be done using multiple methods. When you can compute or accurately estimate the integral of your function, the optimal way is to use it, aka “Inverse transform sampling”. Briefly:
let’s call
Since we use power laws, the intregral is trivial. if such as , with the masses used to define the IMF:
The trick is to observe that varies between 0 and 1, and that there is a unique mapping between and ( is a bijective function). I spare the proof but we can demonstrate that drawing uniform numbers between 0 and 1 will then give us values that exactly follow the IMF.
In our case, the previous equation is inversible, and once you extract as a function of you’re done.
Your solution¶
import numpy as np
class IMF(object):
"""
Here is one possible implementation, which
let you define an IMF as multiple power-laws
"""
def __init__(self, nI, x, a, massMin=0.1, massMax=120., name=None):
"""__init__ - constructor of the class
Parameters
----------
nI: int
number of definition intervals
x: iterable
interval edges (of len nI + 1)
a: iterable
power-law indexes (of len nI) in units of dN/dM (Salpeter corresponds to -2.35)
massMin: float
minimal mass
massMax:
maximal mass
name: string
optional name
notes
-----
1 - the mass range can be restricted by massMin, massMax while keeping
the official definition.
2 - indexes of the different power-laws are assumed to be in units of
dN/dM, ie, -2.35 corresponds to a Salpeter IMF. However, sometimes
you could find -1.35, which corresponds to an index defined in
terms of dN/dlog(M).
"""
# Store relevant information
# ==========================
self.nIMFbins = nI
self.massinf = np.asarray(x)
self.slope = np.asarray(a)
self.name = name
self.coeffcont = np.zeros(np.size(a))
self.massMin = massMin
self.massMax = massMax
# Make functional form
# ====================
# the first step is to build the functional form of the IMF:
# i.e., make a continuous function and compute the normalization
# continuity
# ----------
# given by: c[i-1] * x[i] ^ a[i-1] = c[i] * x[i] ^ a[i]
# arbitrary choice for the first point, which will be corrected by the
# normalization step.
self.coeffcont[0] = 1.
for i in range(1, nI):
self.coeffcont[i] = (self.coeffcont[i - 1])
self.coeffcont[i] *= (x[i] ** (a[i - 1] - a[i]))
# normalize
# ---------
# depends on the adpoted definition of the IMF indexes:
# either dN/dM or dN/dlog(M). In this example we consider that indexes
# are given in units of dN/dM.
# get the norm : integral(imf(M) dM) = 1 seen as a prob dist. funct."""
self.norm = 1. # will be updated at the next line
self.norm = self.get_enclosed_Nstar(self.massMin, self.massMax)
# Compute the average mass
self.avg = self.get_avg_mass(self.massMin, self.massMax)
def get_enclosed_Nstar(self, Mmin, Mmax):
"""get_enclosed_Nstar - Get the enclosed dN over a given mass range.
Analytic integration, Sum(imf(m) dm)
Note: no extrapolation outside the original mass range definition of the IMF.
keywords
--------
Mmin, Mmax: float, float
lower and upper masses
returns
-------
r: float
enclosed dN within [Mmin, Mmax]
"""
x = self.massinf
a = self.slope
c = self.coeffcont
# will be useful in the integration
b = a + 1.
val = 0.
# analytical integration of a power law
for i in range(0, self.nIMFbins):
if (Mmin < x[i + 1]) & (Mmax > x[i]):
if x[i] <= Mmin:
x0 = Mmin
else:
x0 = x[i]
if x[i + 1] <= Mmax:
x1 = x[i + 1]
else:
x1 = Mmax
# careful if the index is 1
if a[i] == 1:
S = c[i] * (np.log(x1) - np.log(x0))
else:
S = c[i] / b[i] * ( (x1) ** (b[i]) - (x0) ** (b[i]) )
val += S
return val * self.norm
def get_enclosed_mass(self, Mmin, Mmax):
"""get_enclosed_mass - Get the enclosed mass over a given mass range.
Analytic integration, integral(m * imf(m) dm)
Note: no extrapolation outside the original mass range definition of the IMF.
Parameters
----------
Mmin, Mmax: float, float
lower and upper masses
returns
-------
r: float
enclosed mass within [Mmin, Mmax]
"""
x = self.massinf
a = self.slope
c = self.coeffcont
# will be useful in the integration
b = a + 2.
val = 0.
# analytical integration of a power law
for i in range(0, self.nIMFbins):
if (Mmin < x[i + 1]) & (Mmax > x[i]):
if x[i] <= Mmin:
x0 = Mmin
else:
x0 = x[i]
if x[i + 1] <= Mmax:
x1 = x[i + 1]
else:
x1 = Mmax
# careful if the index is 1
if a[i] == 2:
S = c[i] * (np.log(x1) - np.log(x0))
else:
S = c[i] / b[i] * ( (x1) ** (b[i]) - (x0) ** (b[i]) )
val += S
return val * self.norm
def getValue(self, m):
"""getValue - returns the value of the normalized IMF at a given mass m
IMF(m) = 1 / norm * c * m ** a
and integral( IMF(m) dm ) = 1
Parameters
----------
m: float or iterable of floats
masses at which evaluate the function
returns
-------
r: float or ndarray(dtype=float)
evaluation of the function (normalized imf)
"""
# if m is iterable
if getattr(m, '__iter__', False):
return np.asarray([ self.getValue(mk) for mk in m])
else:
# extrapolation
if (m > self.massMax) or (m < self.massMin):
return 0.
# exact value exists
elif m in self.massinf[:-1]:
ind = np.where(m == self.massinf)
return float(float(self.coeffcont[ind]) / self.norm * m ** self.slope[ind])
# otherwise do the evaluation with the correct interval
else:
i = 0
if self.nIMFbins > 1:
while m > self.massinf[i]:
i += 1
i -= 1
if self.massinf[i] > self.massMax:
return 0.
else:
return float(float(self.coeffcont[i]) / self.norm * m ** self.slope[i])
def get_avg_mass(self, Mmin, Mmax):
""" get the avg mass over a given range
< M > = integral(M * imf * dM) / integral(imf * dM)
:param Mmin: float, lower mass
:param Mmax: float, upper mass
"""
return self.get_enclosed_mass(Mmin, Mmax) / self.get_enclosed_Nstar(Mmin, Mmax)
def random(self, N, massMin=None, massMax=None):
"""random - Draw mass samples from this distribution
Samples are distributed over the interval [massMin, massMax]
Interval is truncated to the IMF range definition if it extents beyond it. (taken as is otherwise)
Parameters
----------
N: int
size of the sample
massMin: float
lower mass (default self.massMin)
massMax: float
upper mass (default self.massMax)
returns
-------
r: ndarray(dtype=float)
returns an array of random masses
method
------
drawing random numbers from a given distribution can be done using
multiple methods. When you can compute or accurately estimate the
integral of your function, the optimal way is to use it, aka "Inverse
transform sampling". Briefly:
let's call F(x) = integral( imf(m) dm, m=massMin..x)
Since we use power laws, the intregral is trivial. if x such as
M[i] <= x < M[i+1], with M the masses used to define the IMF:
F(x) = F(M[i]) + 1 / norm * 1 / (a[i] + 1) ( x ** (a[i] + 1) - M[i] ** (a[i] + 1) )
The trick is to observe that F(x) varies between 0 and 1, and that
there is a unique mapping between F(x) and x (F is a bijective
function).
I spare the proof but we can demonstrate that drawing uniform F(x)
numbers between 0 and 1 will then give us x values that exactly follow
the imf.
In our case, the previous equation is inversible, and once you extract
x as a function of F(x) you're done.
"""
# check keyword values, default is the IMF definition
massMin = massMin or self.massMin
massMax = massMax or self.massMax
beta = self.slope + 1.
# compute the cumulative distribution values at each mass interval edge
F = np.zeros(self.nIMFbins + 1)
F[-1] = 1.0
for i in range(1, self.nIMFbins):
F[i] = F[i - 1] + 1. / self.norm * (self.coeffcont[i - 1] / (beta[i - 1])) * ( self.massinf[i] ** (beta[i - 1]) - self.massinf[i - 1] ** (beta[i - 1]) )
#find intervals of massMin and massMax
for k in range(self.nIMFbins):
if massMin >= self.massinf[k]:
mink = k
if massMax >= self.massinf[k]:
maxk = k
if massMin < self.massMin:
Fmin = 0.
elif massMin >= self.massMax:
return
else:
i = mink
Fmin = F[i] + 1. / self.norm * ( self.coeffcont[i] / (beta[i]) ) * ( massMin ** (beta[i]) - self.massinf[i] ** (beta[i]) )
if massMax >= self.massMax:
Fmax = 1.0
elif massMax < self.massMin:
return
else:
i = maxk
Fmax = F[i] + 1. / self.norm * ( self.coeffcont[i] / (beta[i]) ) * ( massMax ** (beta[i]) - self.massinf[i] ** (beta[i]) )
x = np.random.uniform(Fmin, Fmax, N)
y = np.zeros(N)
for k in range(self.nIMFbins):
ind = np.where((x >= F[k]) & (x < F[k + 1]))
if len((ind)[0]) > 0:
y[ind] = self.massinf[k] * ( 1. + (x[ind] - F[k]) / (self.massinf[k] ** (beta[k])) * ( beta[k] ) * self.norm / self.coeffcont[k]) ** (1. / (beta[k]))
return y
def __call__(self, m=None):
"""__call__ - make a callable object (function like)
Parameters
----------
m: float or iterable or None
if None calls self.info()
else calls self.getValue(m)
"""
if m is None:
return self.info()
return self.getValue(m)
def info(self):
""" prints a quick summary of the functional object """
txt = """IMF: {s.name}, IMF(m) = 1./norm * c * m ** a
nI = {s.nIMFbins},
norm = {s.norm}, 1/norm = {invnorm},
Average mass = {s.avg},
m[] = {s.massinf},
a[] = {s.slope},
c[] = {s.coeffcont}"""
print(txt.format(s=self, invnorm=1. / self.norm))
# Deriving common IMF from the literature
#=========================================
# in the definitions below, power-law indexes are given for the dN/dlog(M)
# definition and accordingly converted before usage
class Kennicutt(IMF):
def __init__(self):
nI = 2
x = [0.1, 1., 120.]
a = [-0.4, -1.5]
a = np.asarray(a) - 1
massMin = 0.1
massMax = 120.
IMF.__init__(self, nI, x, a, massMin, massMax, name='Kennicutt')
class Kroupa2001(IMF):
def __init__(self):
nI = 4
x = [0.01, 0.08, 0.5, 1., 150.]
a = [0.7, -0.3, -1.3, -1.3]
a = np.asarray(a) - 1
massMin = 0.01
massMax = 120.
IMF.__init__(self, nI, x, a, massMin, massMax, name='Kroupa 2001')
class Kroupa93(IMF):
def __init__(self):
nI = 3
x = [0.1, 0.5, 1., 120.]
a = [-0.3, -1.2, -1.7]
a = np.asarray(a) - 1
massMin = 0.1
massMax = 120.
IMF.__init__(self, nI, x, a, massMin, massMax, name='Kroupa 1993')
class Salpeter(IMF):
def __init__(self):
nI = 1
x = [0.1, 120.]
a = [-1.35]
a = np.asarray(a) - 1
massMin = 0.1
massMax = 120.
IMF.__init__(self, nI, x, a, massMin, massMax, name='Salpeter')
class MillerScalo(IMF):
def __init__(self):
nI = 3
x = [0.1, 1., 10., 120.]
a = [-0.4, -1.5, -2.3]
a = np.asarray(a) - 1
massMin = 0.1
massMax = 120.
IMF.__init__(self, nI, x, a, massMin, massMax, name='Miller & Scalo')
class Scalo98(IMF):
def __init__(self):
nI = 3
x = [0.1, 1., 10., 120.]
a = [-0.2, -1.7, -1.3]
a = np.asarray(a) - 1
massMin = 0.1
massMax = 120.
IMF.__init__(self, nI, x, a, massMin, massMax, name='Scalo 1998')
class Scalo86(IMF):
def __init__(self):
nI = 24
x = [ 1.00000000e-01, 1.10000000e-01, 1.40000000e-01,
1.80000000e-01, 2.20000000e-01, 2.90000000e-01,
3.60000000e-01, 4.50000000e-01, 5.40000000e-01,
6.20000000e-01, 7.20000000e-01, 8.30000000e-01,
9.80000000e-01, 1.17000000e+00, 1.45000000e+00,
1.86000000e+00, 2.51000000e+00, 3.47000000e+00,
5.25000000e+00, 7.94000000e+00, 1.20200000e+01,
1.82000000e+01, 2.69200000e+01, 4.16900000e+01,
1.20000000e+02 ]
a = [ 3.2 , 2.455, 2. , 0.3 , 0. , 0. , -0.556, -1.625,
-1.833, -1.286, 1.5 , -1.857, 0. , -2.333, -3.455, -1.692,
-2.571, -1.722, -1.611, -1.667, -2.333, -1.353, -0.947, -1.778]
a = np.asarray(a) - 1
massMin = 0.1
massMax = 120.
IMF.__init__(self, nI, x, a, massMin, massMax, name='Scalo 1986')Plot at least a couple of mass functions on the same figure
imf = Salpeter()
imf.info()IMF: Salpeter, IMF(m) = 1./norm * c * m ** a
nI = 1,
norm = 16.5819640406949, 1/norm = 0.060306487069072975,
Average mass = 0.3534872405601367,
m[] = [1.0e-01 1.2e+02],
a[] = [-2.35],
c[] = [1.]
imf = Kroupa2001()
imf.info()IMF: Kroupa 2001, IMF(m) = 1./norm * c * m ** a
nI = 4,
norm = 0.503249268284521, 1/norm = 1.9870868434817714,
Average mass = 0.37970570399992787,
m[] = [1.0e-02 8.0e-02 5.0e-01 1.0e+00 1.5e+02],
a[] = [-0.3 -1.3 -2.3 -2.3],
c[] = [1. 0.08 0.04 0.04]
logm = np.arange(np.log10(0.1), np.log10(120), 0.1)
m = 10 ** logm
for imf_cls in (Salpeter, Kroupa2001, Kennicutt):
imf = imf_cls()
plt.plot(m, imf(m), label=imf.name, lw=2)
plt.xscale('log')
plt.yscale('log')
plt.xlabel(r'mass [M$_\odot$]')
plt.ylabel(r'p(mass | IMF)')
plt.legend()
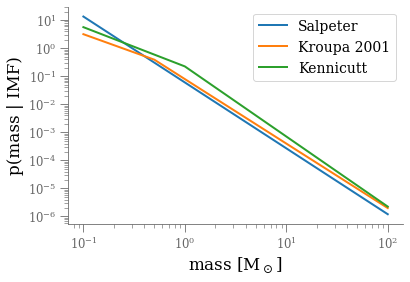
Draw a random sample of N masses from one mass function and show that the sample follows the desired distribution
imf = Kroupa2001()
rvs = imf.random(10_000) #10000 10_000
_, b, _ = plt.hist(np.log10(rvs), log=True,
bins=128, density=True, alpha=0.5)
c = 0.5 * (b[1:] + b[:-1])
dm = np.diff(10 ** b)
plt.plot(c, imf(10 ** c) * dm / (b[1] - b[0]), lw=3)
Decorators¶
A simple syntax for calling “higher-order functions”.
def say_hello(name: str) -> str:
return f"Hello {name:s}"
def be_awesome(name: str) -> str:
return f"Yo {name:s}, together we are the awesomest!"
def greet_bob(greeter_func: Callable) -> str:
return greeter_func("Bob")greet_bob(say_hello)'Hello Bob'greet_bob(be_awesome)'Yo Bob, together we are the awesomest!'ℹ️ greet_bob takes a function as argument. In Python, functions can be passed around and used as arguments
Inner Functions¶
def parent() -> None:
print("Printing from the parent() function")
def first_child() -> None:
print("Printing from the first_child() function")
def second_child() -> None:
print("Printing from the second_child() function")
second_child()
first_child()parent()Printing from the parent() function
Printing from the second_child() function
Printing from the first_child() function
ℹ️ inner functions are local variables (scope dependent).
Returning functions from functions¶
As any other variable, Python allows you to use functions as return values.
def parent() -> Callable:
def inner() -> str:
return "Hi, I am the inner function"
return innerparent()<function __main__.parent.<locals>.inner() -> str>parent()()'Hi, I am the inner function'A first useless decorator¶
a decorator wraps a function into a function
def deco(func: Callable) -> Callable:
def wrapper(*args, **kwargs):
print(f"Something before calling the function.")
result = func(*args, **kwargs)
print("Something after calling the function.")
return result
return wrapper
def say_whee():
print("Whee!")
say_whee = deco(say_whee)Can you guess what happens when you call say_whee()?
say_whee()Something before calling the function.
Whee!
Something after calling the function.
What happened?
>>> say_whee = deco(say_whee) # decoration of `say_whee`
>>> say_whee
<function deco.<locals>.wrapper at 0x7f3c5dfd42f0>Syntactic Sugar!
@deco
def say_whee():
print("Whee!")say_whee()Something before calling the function.
Whee!
Something after calling the function.
What’s decorated?¶
help(say_whee)Help on function wrapper in module __main__:
wrapper(*args, **kwargs)
How do we fix this? e.g., propagating documentation --> @functools.wraps
from functools import wraps
def deco(func: Callable) -> Callable:
@wraps(func)
def wrapper(*args, **kwargs):
# Something before
result = func(*args, **kwargs)
# Something after
return result
return wrapperSome useful examples of decorators¶
timeit- gives runtime of a functionmemoize- A quick cachingfunctools.lru_cache- a LRU caching mechanism (built-in)astropy.units.quantity_inputto validate the units of arguments/outputs
a simple timeit¶
from functools import wraps
import time
def timeit(func):
"""Prints the runtime of decorated functions"""
@wraps(func)
def wrapper_timer(*args, **kwargs):
start_time = time.perf_counter()
value = func(*args, **kwargs)
end_time = time.perf_counter()
run_time = end_time - start_time
print(f"Finished {func.__name__!r} in {run_time:.4f} secs")
return value
return wrapper_timer
@timeit
def waste_some_time(num_times):
for _ in range(num_times):
sum([i**2 for i in range(10000)])
waste_some_time(999)Finished 'waste_some_time' in 3.3324 secs
A quick caching memoize¶
import functools
class memoize(dict):
'''Caches a function's return value each time it is called
and returns the cached value when called later with the same arguments. (not reevaluated).
'''
def __init__(self, func):
self.func = func
functools.update_wrapper(self, func)
def __getitem__(self, *key):
return dict.__getitem__(self, key)
def __missing__(self, key):
ret = self[key] = self.func(*key)
return ret
__call__ = __getitem__
@memoize
def fibonacci(n):
"Return the nth fibonacci number."
if n in (0, 1):
return n
return fibonacci(n-1) + fibonacci(n-2)%timeit fibonacci(30)169 ns ± 0.754 ns per loop (mean ± std. dev. of 7 runs, 10,000,000 loops each)
built-in LRU cache decorator¶
speed up consecutive runs of functions and operations using cache
from functools import lru_cache
@lru_cache
def factorial(n):
return n * factorial(n-1) if n else 1%timeit factorial(20)48.8 ns ± 0.661 ns per loop (mean ± std. dev. of 7 runs, 10,000,000 loops each)
Numba Jit¶
The Numba package provides the jit decorator, which makes running more intensive software a lot easier without having to drop into C.
from numba import jit
import random
@jit(nopython=True)
def monte_carlo_pi(nsamples):
acc = 0
for i in range(nsamples):
x = random.random()
y = random.random()
if (x ** 2 + y ** 2) < 1.0:
acc += 1
return 4.0 * acc / nsamplesmonte_carlo_pi(100_000)3.14064import astropy.units as u
@u.quantity_input(myangle=u.arcsec)
def myfunction(myangle):
return myangle ** 2
@u.quantity_input
def myfunction(myangle: u.arcsec):
return myangle ** 2
@u.quantity_input
def myfunction(myangle: u.arcsec) -> u.deg ** 2:
return myangle ** 2# Test hereStacking decorators¶
@timeit
@lru_cache
def fibonacci(n):
"Return the nth fibonacci number."
if n in (0, 1):
return n
return fibonacci(n-1) + fibonacci(n-2)#Test here@lru_cache
@timeit
def fibonacci(n):
"Return the nth fibonacci number."
if n in (0, 1):
return n
return fibonacci(n-1) + fibonacci(n-2)#test here⚠️ Ordering matters!
Context managers¶
objects that defines the runtime context
An example: open, process, and close a file/buffer¶
%%file foo.txt
Lorem ipsum dolor sit amet, ea feugiat maiorum evertitur his. Rebum molestie scriptorem ad eam, duo posse nostro scaevola te. Vix dolorum iudicabit ad. Verear utamur vulputate eum id, ius ad ocurreret euripidis, eu qui dicant tritani fierent. Eam in latine voluptaria, erant audiam tacimates ea nec, iisque eripuit vim at.
An pri illum prodesset, sit no vocent imperdiet conclusionemque. Et has erat mediocritatem conclusionemque. Vel sint ferri sapientem ne. Quaeque scriptorem ius in, soleat adipiscing intellegam in duo, pro inani doctus facilis cu.
Pri ut mentitum necessitatibus, nulla labores perfecto sea te. At atqui aliquam his, est te meis percipit adipisci, atqui ocurreret ut pro. Ei pri vero explicari dissentias, vitae epicurei quaerendum nam ad, ut nam autem tation patrioque. Nibh eligendi maluisset eos ut, usu et utinam vidisse percipitur.
At wisi probo vel, et nostrum epicurei definiebas pri, an homero neglegentur reprehendunt has. Eu saepe oblique his, et vidisse detraxit mei. Unum vituperata duo ei, rebum deseruisse dissentiunt eum ne. Mel cu vitae salutatus tincidunt. Dictas utamur quo in, ei has percipit consequat.
Eu populo mentitum vis, esse alienum offendit ex nam, sea an ullum quando moderatius. Vis suscipit pertinacia te, ea ius nominavi iudicabit, cu congue veniam pri. Sea quot prompta reformidans at, dicat tractatos pri ne. Sed modo audire ne, dolor prompta eum cu. An duo etiam elaboraret interesset, te mea zril recteque. Equidem maiorum elaboraret id vis.fp = open("foo.txt", 'r')
for line in fp:
# do something
print(line[:10], '...')
fp.close() After many lines, I commonly forget to clean up and close the file. But with a context manager, I can automatically close the file
with open('foo.txt', 'r') as fp:
for line in fp:
# do something
print(line[:10], '...')
fp.seek(0)What are context managers?¶
Context managers are normally invoked using the with statement
A context manager handles the entry into, and the exit from, a desired runtime context for the execution of the block of code.
class MyContext:
def __enter__(self):
"""Enter the runtime context related to this object.
Must return the target(s) specified in the `as` clause of the statement, if any."""
...
return self # typically
def __exit__(self, exc_type, exc_value, traceback):
"""Exit the runtime context related to this object.
The parameters describe the exception that caused the context to be exited (or None)"""
passCommon Usage¶
close the file/socket/buffer handle (even if you crash)
commit transactions (even if you crash)
release a lock
restore initial values (stateful APIs)
user interaction (e.g. logger, progress, profiling)
from contextlib import suppress
import os
with suppress(FileNotFoundError):
os.remove('foo.txt')Excercise: write a timeit context manager¶
# your code heredef fibonacci(n):
"Return the nth fibonacci number."
if n in (0, 1):
return n
return fibonacci(n-1) + fibonacci(n-2)
with timeit("Fibonacci"):
fibonacci(40)
# stdout/stderr something like
# "'Fibonacci' execution time: 32.6sWhat about caching the fibonacci function?
💡 you can reuse the decorators from before.